1. Cauchy-Schwarz Inequality
\[ |\mathbb{E}[XY]| \leq \sqrt{\mathbb{E}[X^2] \mathbb{E}[Y^2]} \]
(\(X\)와 \(Y\)가 uncorrelated이라면 굳이 이런 inequality 쓸 필요없이 바로 구해주면 됨.)
\[ \mathbb{E}[XY] = \mathbb{E}[X] \mathbb{E}[Y] \]
이 부등식은 사실 correlation이 -1에서 1사이다 랑 같은 부등식임. X,Y의 mean = 0이라고 가정하고 식을 유도해보면 코시 슈바르츠 부등식과 똑같은 식이 나온다.
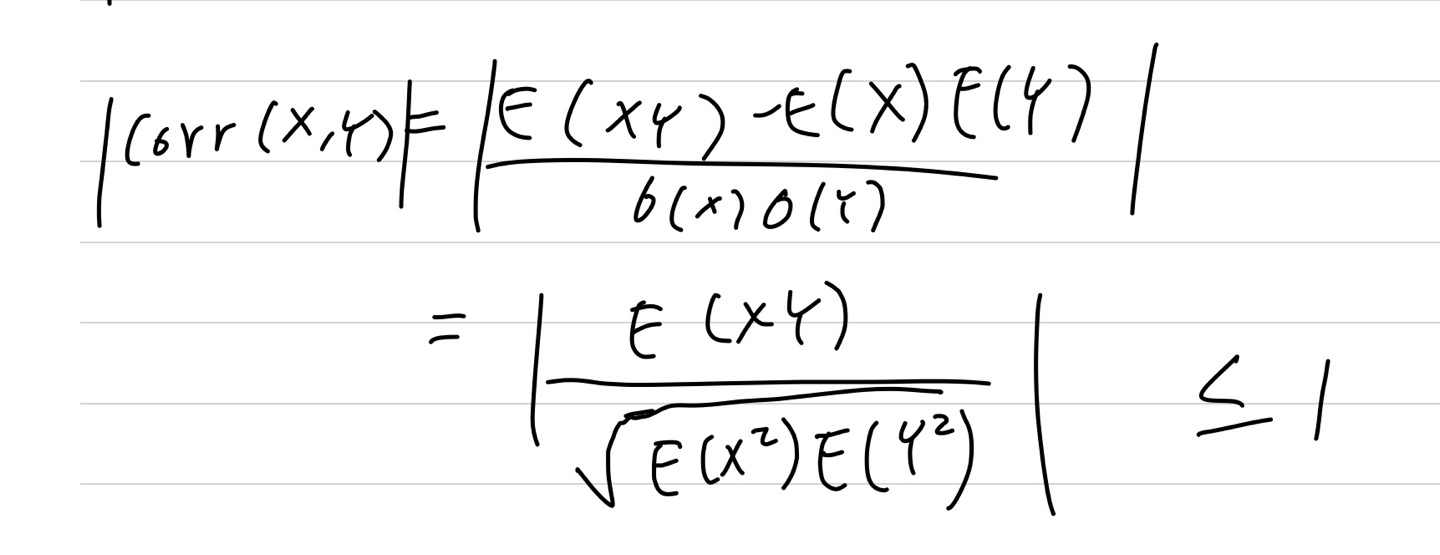
2. Jensen's Inequality
\(f(x)\)가 convex라면 다음 부등식이 성립한다.
\[ f(\mathbb{E}[X]) \leq \mathbb{E}[f(X)] \]
볼록함수면 어떤 접선을 그어도 항상 그 위에 함수가 있어야하니까 이걸 부등식으로 써서 잘 정리해 주면 위의 부등식이 나온다.
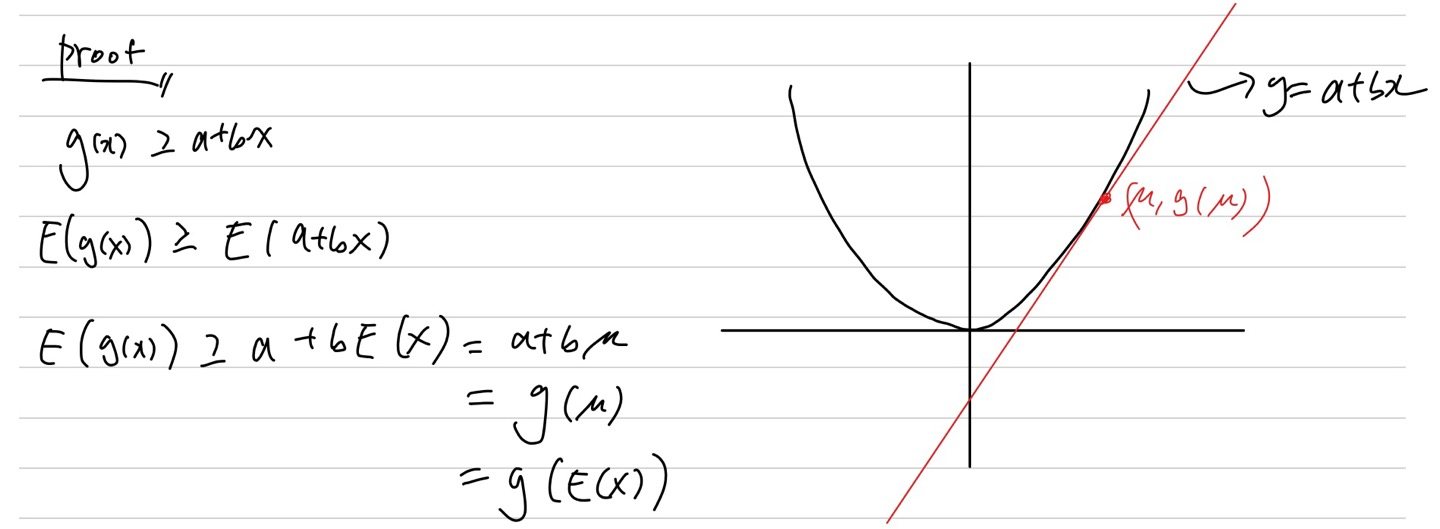
3. Markov's Inequality
\[ P(|X| \geq a) \leq \frac{\mathbb{E}[|X|]}{a}, \quad (a > 0) \]

이 식이 직관적으로 무슨 의미인지 생각해보자.
100명의 사람의 수입을 E(X)라고 생각해보면, 50% 이상의 사람들이 평균 수입의 2배보다 수입이 많은 경우가 있을 수 있는가? 생각해보면 절대 아니다.
평균 수입이 \(\mu\) 라면 총합은 \(100\mu\)가 될것인데, 만약 절반의 사람(50명)이 평균 수입의 2배라면 절반의 사람만으로 벌써 \(100\mu\) 가 채워지니까 절대 불가능한걸 알 수 있다.
그래서 마코프 부등식에서 a를 \(2\bar{X}\) 라고 놓고, 생각해보면
\( P(X \geq 2\bar{X}) \leq \frac{\bar{X}}{2\bar{X}} = 0.5\)
평균의 두 배 이상인 값이 나타날 확률은 최대 50프로이다. 따라서 50프로 이상이 평균 수입의 2배를 벌 가능성은 없다고 해석할 수 있다.
4. Chebyshev's Inequality
\[ P(|X - \mu| \geq a) \leq \frac{\text{Var}(X)}{a^2} \quad (\mu = \mathbb{E}[X], \, a > 0) \] 또는 : \[ P(|X - \mu| \geq c \cdot \text{sd}(X)) \leq \frac{1}{c^2} \quad (c > 0) \]

마코프부등식을 이용하면 증명이된다