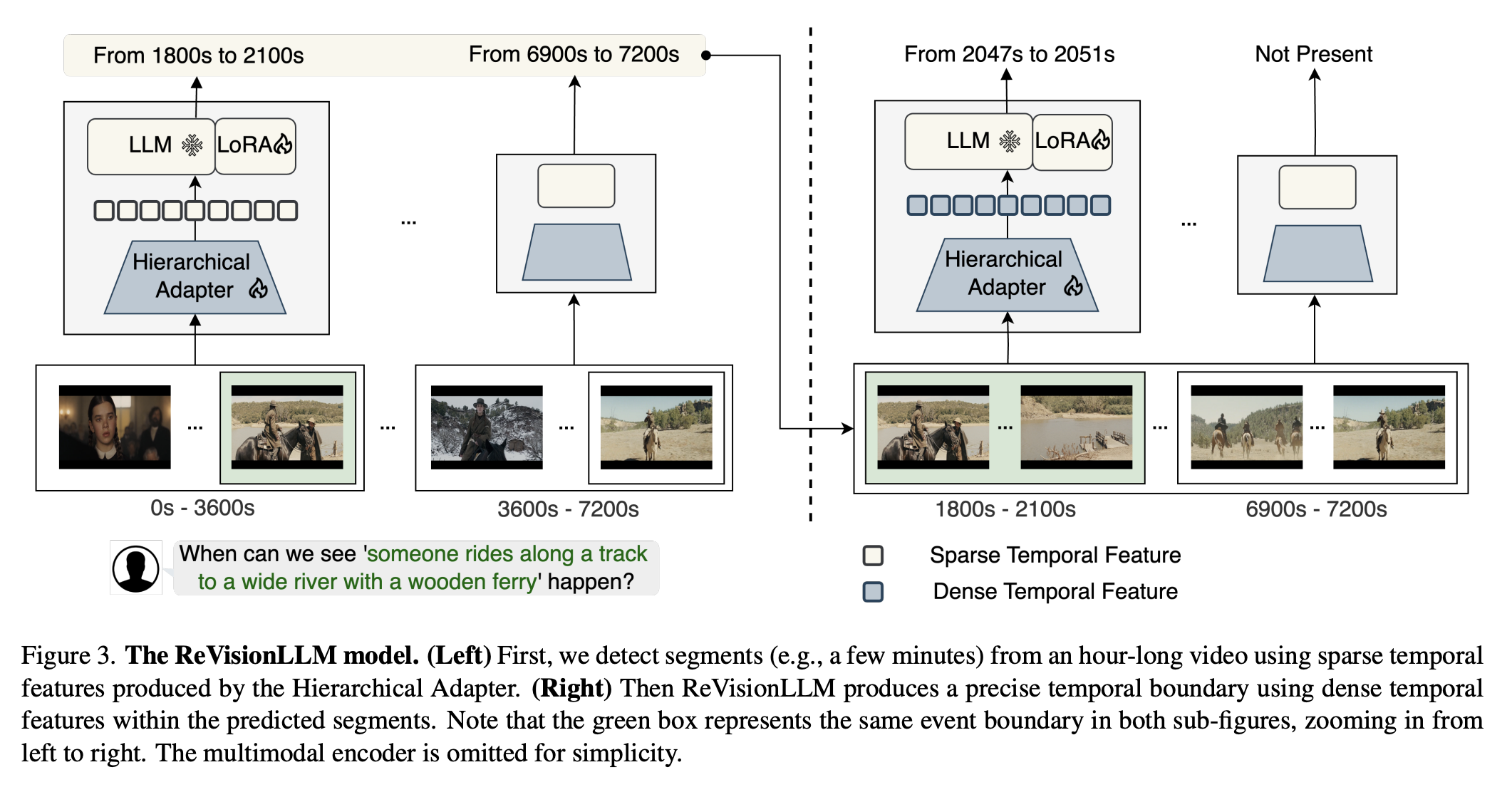
긴 영상에서 ‘언제, 어떤 일이 일어났는지’를 찾아내는 것을 기존 VLM은 잘 못한다. 프레임 수 한계 때문에 중요한 순간이 누락되기 쉽고, 결과적으로 시간 경계가 흐릿해진다. ReVisionLLM은 이 한계를 극복하기 위해 인간이 영상을 훑는 방식을 모방해서 재귀적 탐색 방식을 사용한다.
모델은 먼저 저해상도 전체 scan으로 관심 구간을 대략적으로 지정한다. 이후 해당 구간만 프레임 해상도를 높여 다시 분석하고, 필요하면 더 세밀하게 확대한다. 이렇게 “넓게 → 좁게 → 더 좁게” 과정을 반복하며 최종적으로 초 단위 경계를 산출한다.
훈련 과정도 hierachical 하게 설계한다. 짧은 10–30 초 클립에 먼저 사건 인지 능력을 학습시킨 뒤, 점차 길이를 늘려 몇 시간짜리 영상까지 확장 학습을 진행한다. 이 덕분에 모델은 다양한 길이의 영상을 자연스럽게 처리한다.
Model
Multimodal Encoder
| \(f^{t}\) | 한 프레임의 CLS 임베딩 | \(\mathbb{R}^{D}\) | \(D = 768\) |
| \(F\) | 전체 비디오 시퀀스 \([\!f^{1},\dots,f^{T}\!]\) | \(\mathbb{R}^{T\times D}\) | \(T = 3\,600\) |
| \(Q\) | 쿼리 토큰 임베딩 | \(\mathbb{R}^{N_{s}\times D}\) | \(N_{s}=32\) |
이렇게 두 모달리티가 \(D\) 차원을 공유한다.
Hierarchical Adapter
- 상위 계층에서는 전체 영상(1 h)을 3 분마다 1 토큰으로 압축한 Sparse Feature \(S\)를 사용한다.
이를 통해 “18–21 분 구간에 이벤트 있음”과 같은 대강의 위치를 찾는다. - 하위 계층에서는 이 구간을 원래 프레임 해상도의 Dense Feature \(D\)로 확대하여 “18:32 – 19:07” 식으로 정확한 경계를 예측한다.
정리하자면:
| ① 슬라이딩 윈도 | \(F \rightarrow \{C^{i}\}\) | \(\mathbb{R}^{T\times D}\; \rightarrow\; \mathbb{R}^{L_{w}\times D}\) | 1 시간 시퀀스를 2 분(120 f) 단위로 분할한다. |
| ② Dense 프로젝션 | \(D^{i}=h_{d}(C^{i})\) | \(\mathbb{R}^{L_{w}\times D}\) | 프레임 정보를 그대로 유지한다. |
| ③ Cross-Attn 정렬 | \(\tilde C^{i}=\text{CrossAttn}(C^{i},Q)\) | 동일 Shape | 질문과 연관된 프레임에 가중치를 준다. |
| ④ Self-Attn 압축 | \(S^{i}=A_{0}\) | \(\mathbb{R}^{D}\) | “클립 1개 = 토큰 1개”로 축소한다. |
LLM 입력 & prediction
프롬프트 템플릿
<video> when can we see the <event> happening?
<video> 자리에는 계층별 비디오 피처 \(I^{(\ell)}\)(=\(D\) 또는 \(S\))를 삽입한다.
완성된 입력은 \(P^{(\ell)}=[\,I^{(\ell)}, w_{1},\dots,w_{M}]\) 이 된다.
| \(\ell=1\) | Sparse \(S\) + 프롬프트 | From 120 to 240. 또는 Not Present. |
영상 전체를 훑어 거친 구간을 찾는다. |
| \(\ell>1\) | 직전 결과 구간을 잘라 Dense/Sparse로 변환 후 입력 | From s to e. |
점차 해상도를 높여 경계를 정밀화한다. |
각 계층에서 목표 문장 토큰 시퀀스 \(T^{(\ell)}\)에 대해 $$ \mathcal{L} = -\sum_{k=1}^{K} \log p\!\Bigl( T_{k}^{(\ell)} \;\big|\; T_{\lt k}^{(\ell)},\, P^{(\ell)} \Bigr) $$ 로 loss를 최소화한다.
Training

| Stage 1-A(Dense, 짧은 클립) | • 10–30 초 Positive·Negative 클립에 대해 “From s to e.” 또는 “Not Present.” 생성 | • boundary regression을 먼저 익혀 framing 감각 학습• Negative 클립으로 over-confidence 완화 | LoRA(LLM) + Hier-Adapter 모두 학습 |
| Stage 1-B(Sparse, 짧은 클립) | • LLM 가중치 Freeze 후• Adapter만 학습해 Down-sample 규칙 최적화• 프롬프트: “<video> Does the <event> happen? yes/no” | • Adapter가 “정보를 얼마만큼/어디서 버릴지” 배우게 함• 목표는 존재 여부만 예측 → 문제를 단순화 | Hier-Adapter만 학습 |
| Stage 2(Sparse, 1 h 영상) | • Stage 1-B가 만들어 둔 Sparse 토큰(예: 3 분 간격)으로 1시간 영상을 훑음 • 다시 “From s to e.” 문장 생성 | • Sparse 토큰 덕분에 긴 영상을 검색• 이미 정렬된 피처이므로 LoRA만 파인튜닝해도 충분 | LoRA(LLM) 만 파인튜닝 |
학습 intuitive는
먼저 짧은 클립에서 ‘언제’와 ‘없음’을 확실히 가르친다, 이후 같은 짧은 클립을 다시 보되, 이번엔 어댑터만 학습해 ‘요약 토큰’ 만드는 법을 배운다. 이제 1 시간짜리 영상도, 3 분 간격 Sparse 토큰 20~30개만 보고 대강 위치를 찍을 수 있다. 필요하면 Stage 2가 찾아낸 구간을 다시 Dense 피처(=Stage 1-A 방식)로 확대해 프레임 단위 경계까지 정밀화한다.
Inference with Calibrated Confidence
ReVisionLLM은 CLIP 유사도 대신 LLM 자체의 확신 정도로 후보 경계들을 reorganize한다. 이를 위해 예측 문장에 대한 entrophy기반 confidence를 다음과 같이 계산한다.
- 단어-단위 entrophy를 구한다.
$$ H^{(i)}_k = -\sum_{w} p\!\bigl(w\,\big|\,T_{<k},\,\mathcal D^{(i)}\bigr)\; \log p\!\bigl(w\,\big|\,T_{<k},\,\mathcal D^{(i)}\bigr) $$ 여기서 \(p(w\,|\,\cdot)\)은 k 번째 단어를 생성할 확률 분포를 뜻한다. 값이 클수록 모델은 해당 위치에서확신이 없다
고 해석된다. - 문장 전체 entrophy를 평균한다.
$$ \bar H^{(i)} = \frac1K \sum_{k=1}^{K} H^{(i)}_{k} $$ \(K\) 는 생성된 단어 수다. - entrophy의 역수를 취해 신뢰도 \(R^{(i)}\)를 얻는다.
$$ R^{(i)} \;=\; \frac{1}{\displaystyle \frac1K \sum_{k=1}^{K} H^{(i)}_{k}} $$ \(\bar H^{(i)}\)가 작을수록, 즉 확률 분포가 뾰족할수록 \(R^{(i)}\) 값은 커지고 모델이 스스로확신한다
는 뜻이 된다.
모델은 모든 후보 구간에 대해 \(R^{(i)}\)를 계산한다. 그다음 상위 top K만 선택하여 후속 계층 혹은 최종 출력에 사용한다.
