2차원 로터스(2D LOTUS)는 두 개의 랜덤 변수 \(X\)와 \(Y\)가 있을 때, 이들의 결합 분포를 이용하여 \(X\)와 \(Y\)의 함수의 기댓값을 계산하는 방법이다.
2D LOTUS
함수 \(g\)가 \(\mathbb{R}^2 \to \mathbb{R}\)일 때, \(X\)와 \(Y\)가 discrete라면
$$ E(g(X, Y)) = \sum_x \sum_y g(x, y) P(X = x, Y = y) $$
만약 \(X\)와 \(Y\)가 continuous이고, joint pdf \(f_{X,Y}\)를 가지고 있다면,
$$ E(g(X, Y)) = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} g(x, y) f_{X,Y}(x, y) \, dx \, dy $$
그럼 이걸 어디에 쓰냐!
X, Y가 독립일 때 \(E(x,y) = E(x)E(y)\)라는 증명을 아주 쉽게 할 수 있다.
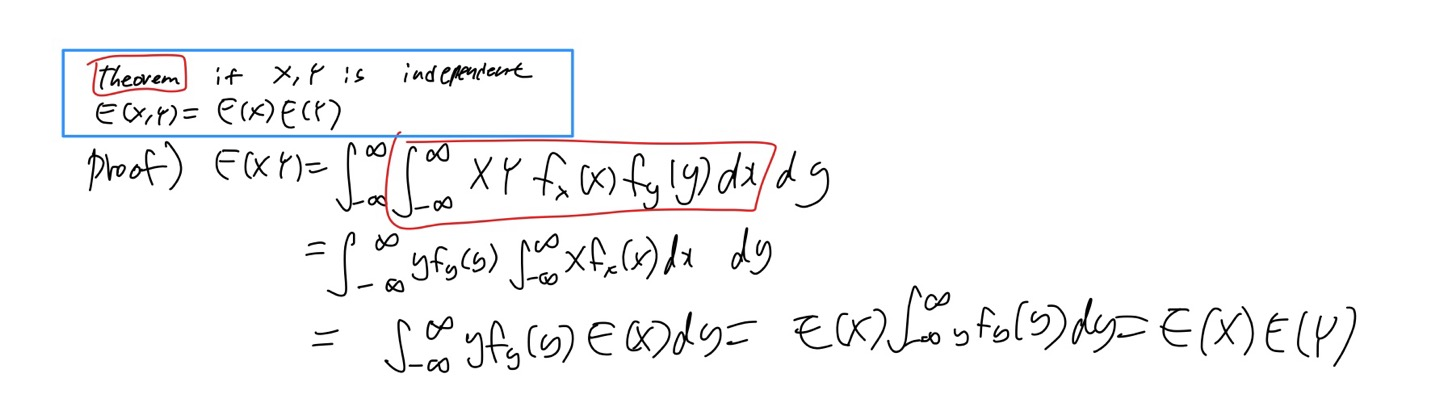
또 두개의 random variable사이의 expected distance를 구하는데 쓸 수도 있다.
X, Y가 \( \sim \text{Unif}(0,1) \)을 따를 때 \( E|X-Y| \) 를 구하기 위해 2D LOTUS를 사용하면 쉽게 구할 수 있다.
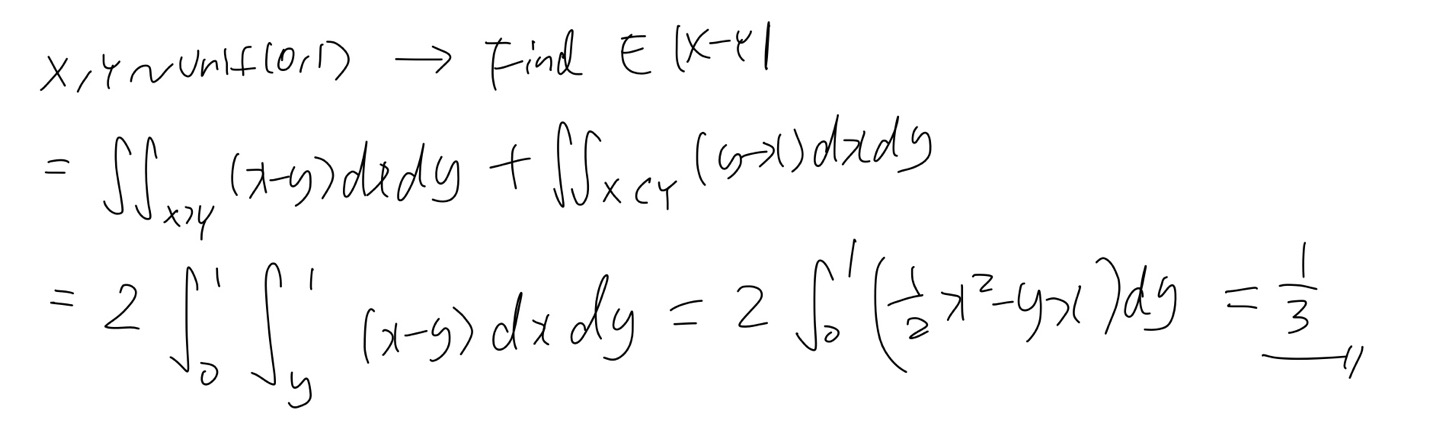
이 문제는 max랑 min의 문제로도 접근 가능하다.
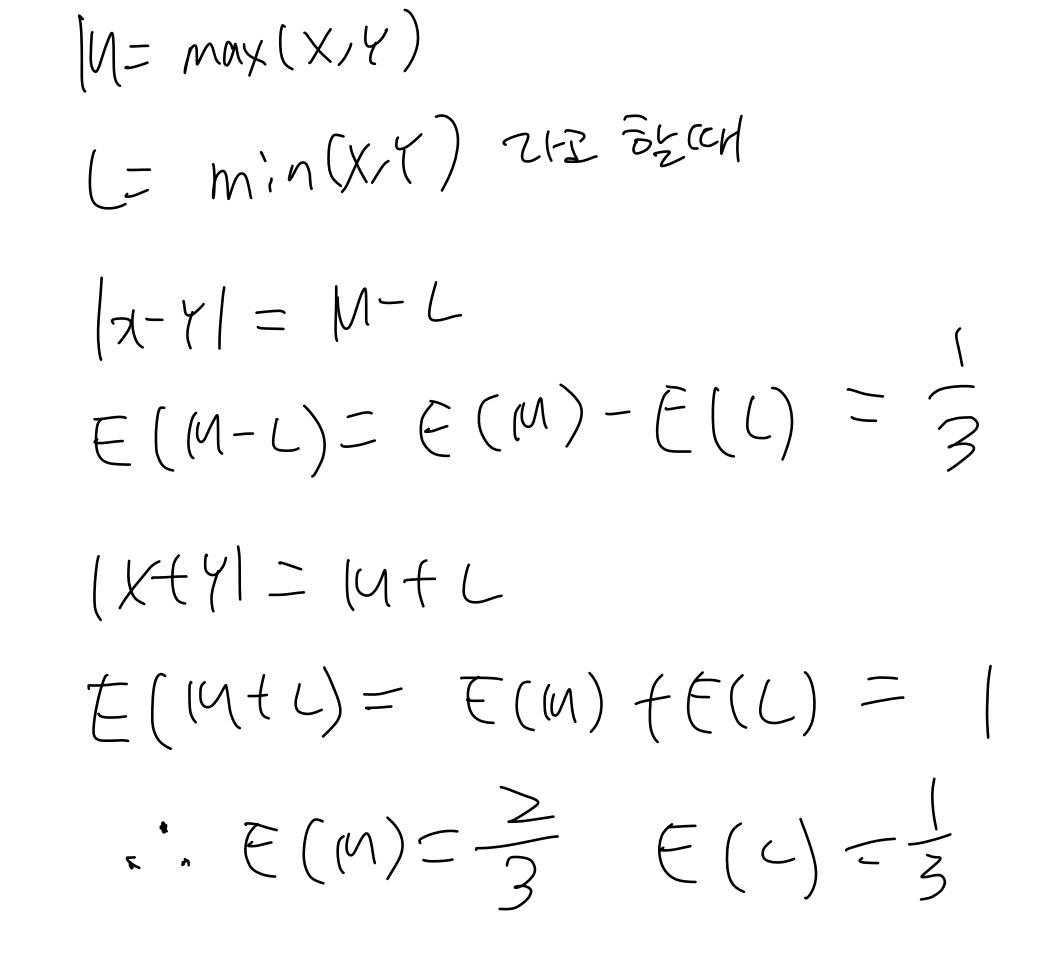
증명은 아니지만 좀 더 직관적으로 생각해보면 0에서 1 사이에 두 개의 random 변수를 고른다고 했을 때 x랑 y지점이 평균적으로 이렇게 생길 것이고, 평균적으로 간격이 1/3일 거는 분명하다.
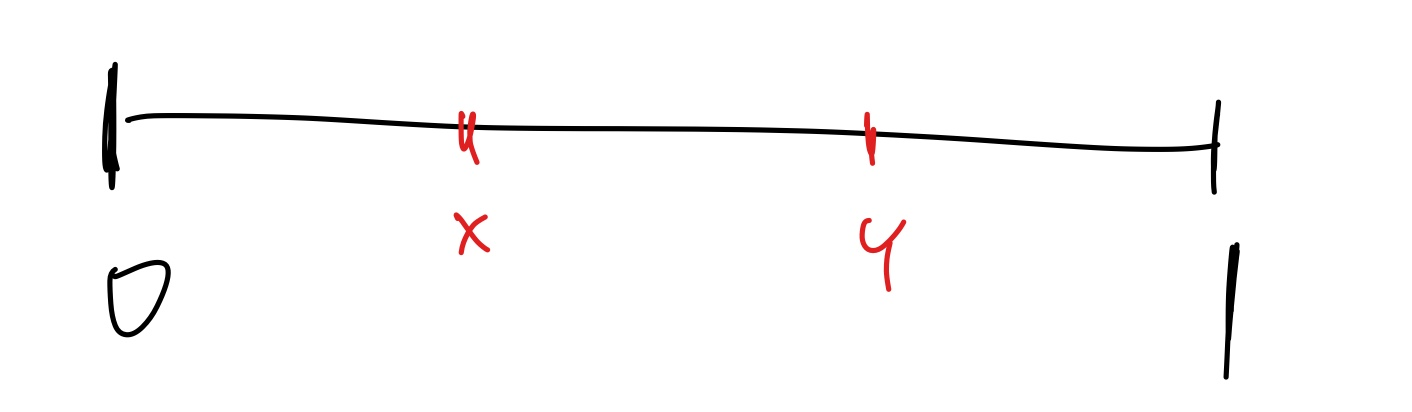
이 내용은 Introduction to Probability (Joseph K. Blitzstein and Jessica Hwang) 책을 읽고 정리한 내용입니다.