VAE에 대해 이해하기전에 autoencoder부터 보면
Autoencoder?
Autoencoder 기본 구조
오토인코더는 입력 데이터 X를 받아 더 낮은 차원의 latent representation Z로 인코딩한 뒤, 이를 다시 입력 데이터와 같은 차원의 출력 X′로 복원하는 신경망 구조이다. 크게 두부분으로 나뉘는데,
- 인코더 : 입력 데이터 X를 받아 잠재 표현 Z로 변환
- 디코더(Decoder): 잠재 표현 Z를 받아 원본 데이터와 유사한 데이터 X′로 복원함
오토인코더의 한계
전통적인 오토인코더는 데이터의 잠재 표현 Z를 어떻게 사용해 새로운 샘플을 생성할지에 대한 명확한 방법이 없고, 잠재 공간의 분포에 대한 가정이 없기 때문에, 잠재 변수 Z에서 샘플을 임의로 추출하여 의미 있는 새로운 데이터를 생성하기 어렵다.
그래서 새로운 데이터에 대해서 reconstruction이 어렵고, 때문에 학습을 위해 encoder decoder 다 가져다 쓰지만, 실제로 쓰이는건 encoder.
Variational Auto Encoder?

VAE는 이러한 한계를 극복하기 위해 잠재 공간의 분포에 대한 가정을 도입했음. VAE는 잠재 변수 Z가 특정 확률 분포(예: 가우시안 분포)를 따른다고 가정한다.
- 인코더: 입력 데이터 X로부터 잠재 변수 Z의 분포의 매개변수(평균이나 분산등)를 예측한다. 이를 통해 잠재 공간에서 각 데이터 포인트 주변의 분포를 모델링한다.
- 디코더: 잠재 공간에서 샘플링된 잠재 변수 Z를 사용해 원본 데이터를 복원하려고 시도한다
VAE의 핵심은 인코더가 예측한 분포로부터 잠재 변수 Z를 샘플링해서, 이 샘플을 사용해 디코더가 원본 데이터와 유사한 새로운 데이터를 생성할 수 있도록 하는것.
이 과정은 또한 데이터가 잠재 공간에 어떻게 배치되는지를 학습하게 하며, 이를 통해 새로운 데이터를 생성할 때 잠재 공간에서 의미 있는 점을 선택할 수 있게 됨.
즉 VAE를 image generation에 쓰기 위해서, 만약 z의 분포를 알 수 있다면 디코더 부분을 학습시킬 수 있으니까 디코더를 이용한 generation이 가능해질 것임. 즉, VAE는 p(z)가 N(0,1)임을 가정하고, kl-divergence loss를 통해서 실제 인코더에서 학습시킨 q(z|x) 가 p(z)와 비슷해지도록 한게 핵심 포인트임.
How to Train VAE?
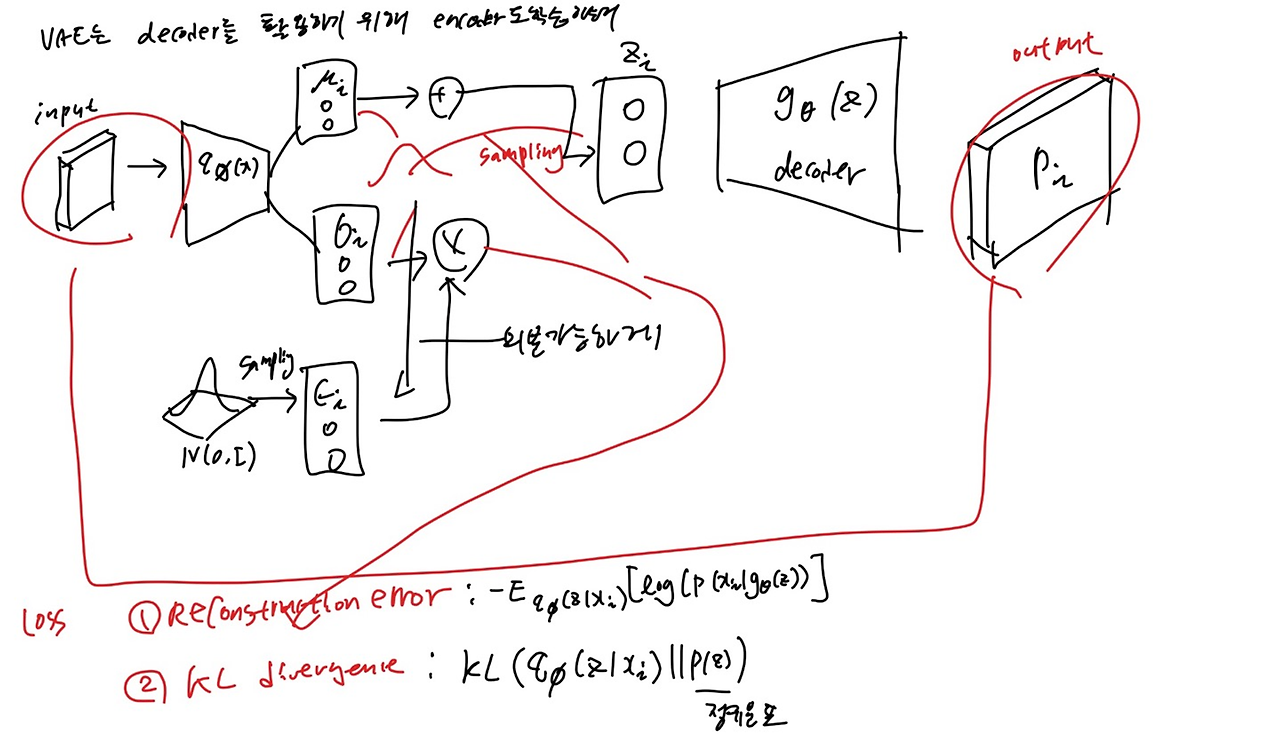
전체적인 구조는 다음과 같다
Auto Encoder와는 다르게, Reconstruction error 뿐만 아니라, encoder 에서 뽑아낸 분포가 얼마나 정규분포와 닮았는지에 대한 KL Divergence도 함께 loss값으로 쓴다.
Loss 함수 유도과정

마지막 무시 부분이, 저부분도 구할수 있으면 당연히 더 정확하고 좋겠지만, 아쉽게도 p(z|x)가 intractable해서 구할 수 없음. 근데 마침 저게 kl divergence이고, 항상 0 보다 크다는 성질때문에, 저 식을 제외 한 나머지 부분이 ELBO로 lower bound가 되는 것이다.

실제 loss 함수는 아까 구한거에서 마이너스를 씌워서, 그걸 최소화시키도록 학습시키면 되는것. 중간에 빨간 부분이 좀 의아한 부분이긴 한데, monte carlo에 따라 식을 저렇게 바꿔 쓸수 있다는데, Monte carlo가 L이 충분이 클때 성립하는걸로 알고 있는데, 논문에서는 그냥 1로 해버린것 같음..
Reparameterization Trick
랜덤 노이즈에서 mu랑 시그마를 직접 얻으려고 하는것보다, learn the parameter to transform

이렇게 해주는 이유는, sampling이 미분 가능한 연산이 아니라서, 미분이 되게 하기 위해 조그만한 trick 을 써준건데
원래는 z가 z∼qϕ(z|x) 에서 (인코더) 직접 샘플링 되었기 때문에 stochasticity 즉, 모델의 작동 과정에 무작위성이 포함되니까 미분이 불가능함.
정리해보자면,
그래서 직관적으로 이해해보자면, 무작위성을 모델의 입력으로부터 분리시키는 trick이라고 볼 수 있음.
z가 인코더를 거친 distribtion에서 바로 샘플링한 stochasitc한 변수였다면, reparameterize trick을 거치고 나면, ϵ∼N(0,I)에서 sampling한 ϵ에 대해 z=μ(X)+Σ1/2∗ϵ이라고 나타낼 수 있게 되는 것.
이렇게 하면 z는 (μ,Σ)에 대해 미분이 가능해짐
구현 코드( https://www.notion.so/VAE-code-83d8481634584392af5a9c1ea5461a84?pvs=4)
노션에 코드까지 함꼐 정리되어있습니다